IMPLIKASI TEORI BELAJAR KONSTRUKTIVISME DALAM PEMBELAJARAN MATEMATIKA

Implikasi Teori Belajar Konstruktivisme dalam Pembelajaran Matematika. Fokus utama dari belajar metematika adalah memberdayakan siswa untuk berpikir dalam mengkonstruksi pengetahuan matematika yang pernah ditemukan para ahli, bukan menjalankan pengetahuan prosedural yang telah ditemukan oleh para ahli matematika sebelumnya. 

Dengan kata lain dari sudut pandang konstruktivis, Koehler and Grouws (TIM MKPBM UPI, 2001) menyatakan bahwa pembelajaran telah dipandang sebagai suatu kontinum antara negosiasi dan imposition pada ujung-ujungnya.

Seseorang yang memandang bahwa belajar adalah suatu transmisi, maka proses mengetahui akan mengikuti model imposition (pembebanan). Sedangkan yang berpandangan bahwa mengajar adalah suatu proses yang memfasilitasi suatu konstruksi, maka ia akan mengikuti model negosiasi.

A. Imposition dan negosiasi

Imposition dan negosiasi ini merupakan dua hal yang berbeda dan sama pentingnya. Dimana proses imposition berguna bagi Pendidik dalam mengkomunikasikan simbol-simbol sederhana dalam matematika sementara negosiasi berguna bagi Pendidik dalam mengkomunikasi-kan matematika sebagai suatu konsep.

Selanjutnya dalam tahap implementasi pembelajaran matematika dengan konstruktivis, kita harus memahami aspek-aspek pembelajaran matematika yang berlandaskan teori konstruktivisme. Berkenaan dengan hal itu, Hanbury (1996) mengemukakan sejumlah aspek yang berkaitan dengan pembelajaran matematika, yaitu

1. siswa mengkonstruksi pengetahuan matematika dengan cara mengintegrasikan ide yang mereka miliki,
2. matematika menjadi lebih bermakna karena siswa mengerti,
3. strategi siswa lebih dinilai, dan
4. siswa mempunyai kesempatan untuk berdiskusi dan saling bertukar pengalaman dan ilmu pengetahuan dengan temannya.

Berdasarkan aspek-aspek tersebut, maka semaksimal mungkin implementasi konstruktivisme dalam pembelajaran matematika harus dimulai dari pendidikan dasar bagi anak. Driver dan Bell (Susan, Marilyn dan Tony, 1995) mengajukan karakteristik sebagai berikut:

1. siswa tidak dipandang sebagai sesuatu yang pasif melainkan memiliki tujuan,
2. belajar mempertimbangkan seoptimal mungkin proses keterlibatan siswa,
3. pengetahuan bukan sesuatu yang datang dari luar melainkan dikonstruksi secara personal,
4. pembelajaran bukanlah transmisi pengetahuan, melainkan melibatkan pengaturan situasi kelas,
5. kurikulum bukanlah sekedar dipelajari, melainkan seperangkat pembelajaran, materi, dan sumber.

B. Pembelajaran berdasarkan pengalaman

Bahkan secara spesifik Herman Hudoyo (1998) mengatakan bahwa seseorang akan lebih mudah mempelajari sesuatu bila belajar itu didasari kepada apa yang telah diketahui orang lain. Oleh karena itu, untuk mempelajari suatu materi matematika yang baru, pengalaman belajar yang lalu dari seseorang akan mempengaruhi terjadinya proses belajar matematika tersebut.

Selain penekanan dan tahap-tahap tertentu yang perlu diperhatikan dalam teori belajar konstruktivisme, Hanbury (1996) mengemukakan sejumlah aspek dalam kaitannya dengan pembelajaran matematika, yaitu

1. siswa mengkonstruksi pengetahuan matematika dengan cara mengintegrasikan ide yang mereka miliki,
2. matematika menjadi lebih bermakna karena siswa mengerti,
3. strategi siswa lebih bernilai, dan
4. siswa mempunyai kesempatan untuk berdiskusi dan saling bertukar pengalaman dan ilmu pengetahuan dengan temannya.

Sebuah pengalaman menarik ditunjukan oleh Fadjar Shadiq (2008) yang menyatakan bahwa :

Ketika ia mengajar di salah satu SMA, ia sempat bertanya kepada salah seorang siswa, mengapa ia menyatakan (a + b)2 = a2 + b2 ? Jawabannya adalah karena 2(a + b) = 2a + 2b. ketika ditanyakan, dari mana pendapat itu muncul, apakah dari Pendidik SMP-nya? Ia pun menjawab bahwa pendapat itu bukan dari Pendidiknya namun dari dirinya sendiri.

Alasan yang sama kemungkinan besar akan dilontarkan seorang siswa SMA yang menyatakan sin (a+b) = sin a + sin b. hal ini telah menunjukan bahwa para siswa telah secara aktif menanggapi hal-hal yang menarik perhatiannya. Namun ternyata juga bahwa tanggapannya tersebut telah didasarkan pada pengetahuan yang sudah ada pada struktur kognitif mereka.

Dengan demikian jelaslah sekarang, dari contoh di atas, bahwa siswa sendiri yang membangun pengetahuan atau teori dan teori yang dikemukakan siswa tadi telah didasarkan pada pengetahuan yang ada di dalam benaknya (struktur kognitifnya).

Baca juga Fungsi Alat Permainan Edukatif yang menyenangkan anak

C. Contoh pembelajaran matematika berbasis konstruktivisme

Diungkapkan Uba Umbara (2017) yaitu pada materi segi empat dalam menentukan keliling persegi panjang, adalah sebagai berikut.

1. Sediakan huruf A, B. C dan D pada kertas ukuran A4.
2. Sediakan rol meteran dengan panjang minimal 50 meter.
3. Ajak siswa ke lapangan yang ada di sekolah, misalnya lapangan basket. Lapangan basket merupakan contoh persegi panjang.
4. Satu orang siswa diminta untuk berjalan mengelilingi lapangan bola basket. Selanjutnya siswa tersebut untuk menaruh huruf yang telah disediakan sebelumnya.
5. Dua orang siswa diminta untuk mengukur panjang dari titik A ke titik B, dari titik B ke titik C, dari titik C ke titik D dan dari titik D ke titik A. sementara siswa lain diminta untuk menulis panjang/jarak dari masing-masing titik tersebut.
6. Setelah diketahui panjang masing-masing titik, mintalah masing-masing siswa untuk menjumlahkan hasil pengukuran. Sehingga di dapat penjumlahan : 28 + 15 + 28 + 15 = 86
7. Setelah itu, minta siswa untuk menyederhanakan penjumlahan tersebut, sehingga di dapat (2 x 28) + (2 x 15) = 86.
8. Pendidik memberikan penjelasan tentang arti panjang dan lebar. Sehingga penyederhanaan penjumlahan tadi bisa diganti menjadi 2P + 2L = K.
9. Penjelasan tersebut dapat dipahami dengan gambar berikut. 

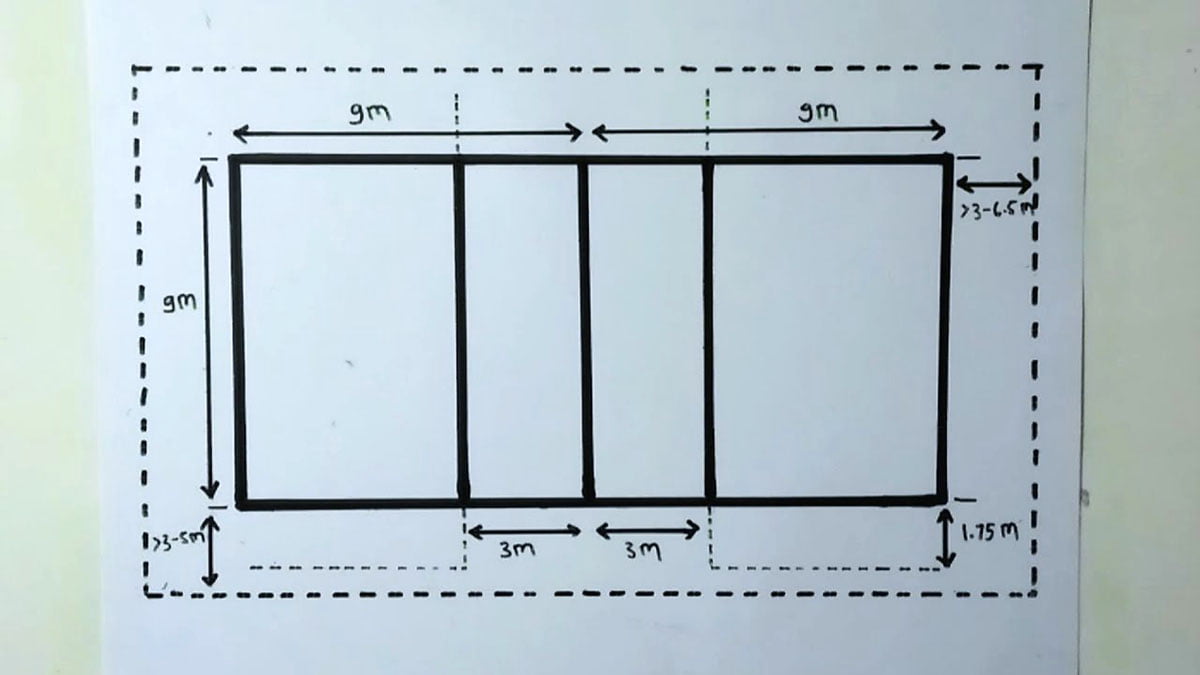
D. Pengajar sebagai Fasilitator

Implikasi Teori Belajar Konstruktivisme dalam Pembelajaran Matematika. Contoh di atas menunjukkan peran Pendidik sebagai seorang fasilitator dalam membantu siswanya agar dapat dengan mudah mengkonstruksi sendiri pengetahuan tentang konsep keliling.

Perintah Pendidik kepada siswa untuk mengelilingi lapangan basket akan memberikan analogi dan pemahaman yang jelas mengenai keliling suatu bangun datar, inilah yang akan menjadi jembatan bagi siswa dalam memahami mengenai konsep keliling.

Sementara perintah Pendidik untuk menjumlahkan hasil pengukuran dan menyederhanakannya kemudian merubah penyederhanaan menjadi sebuah notasi P dan L merupakan contoh anak menggunakan pengetahuan yang ada di dalam struktur kognitifnya.

Dengan demikian, agar suatu pengalaman baru dapat terkait dengan pengetahuan yang sudah ia miliki, maka proses pembelajaran harus dimulai dari pengetahuan yang sudah ada di dalam pikiran siswa (sudah ada kerangka kognitifnya) ataupun mudah ditangkap siswa (mudah dibangun kerangka kognitifnya).

Namun paling penting dan mendasar, tugas utama seorang Pendidik adalah menjadi fasilitator sehingga proses pembelajaran di kelasnya dapat dengan mudah membantu para siswa untuk membentuk (mengonstruksi) pengetahuan yang baru tersebut ke dalam kerangka kognitifnya.

Implikasi Teori Belajar Konstruktivisme dalam Pembelajaran Matematika. Pembelajaran di atas menunjukkan bahwa pembelajaran dimulai dengan mengajukan suatu masalah di mana ide matematikanya diharapkan dapat muncul dari masalah tersebut, diikuti dengan siswa mendiskusikan cara memecahkan masalah yang ada, diikuti dengan menemukan sendiri (guided reinvention) pengetahuan matematikanya.