Pendekatan matematis dapat digunakan dalam mencari harga dan jumlah keseimbangan apabila data yang kita miliki berbentuk fungsi permintaan dan fungsi penawaran. Untuk mencari harga dan jumlah keseimbangan dari kedua fungsi tersebut, kita menggunakan rumus syarat keseimbangan berikut:
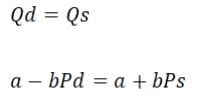
Dimana: Qd = jumlah yang diminta Pd = harga yang diminta Qs = jumlah yang ditawarkan Ps = harga yang ditawarkan.
Contoh : Diketahui :
- Fungsi Permintaan Pasar (D) adalah Qd = 2000 – 50P
- Fungsi Penawaran Pasar (S) adalah Qs = 500 + 25P
Maka Harga Ekulibrium dan Kuantitas Ekuilibrium adalah:

Harga ekulibrium adalah 20 (satuan uang), substitusikan nilai tersebut pada salah satu fungsi permintaan atau penawaran berikut :
Substitusi ke Fungsi Permintaan : Qd = 2000 – 50 P Qd = 2000 – 50 (20) Qd = 1000 unit
Substitusi ke Fungsi Penawaran : Qs = 500 + 25 P Qs = 500 + 25 (20 Qs = 1000 unit
Jadi, kuantitas keseimbangan adalah 1000 unit
Pendekatan matematis dapat digunakan dalam mencari harga dan jumlah keseimbangan, Untuk contoh menghitung harga keseimbangan dapat dilihat juga pada link berikut: https://bit.ly/2FrSYNb.
Baca juga Faktor penentu elastisitas permintaan atas suatu barang ada tiga
Analisis dan Penerapan Harga
Harga adalah faktor kunci dalam kehidupan ekonomi kita. Sebagai konsumen, kita selalu mencari nilai terbaik dan harga yang paling kompetitif saat berbelanja, sementara perusahaan dan produsen berusaha mengoptimalkan harga produk mereka untuk mencapai keuntungan maksimal. Untuk mencapai tujuan ini, pendekatan matematis seringkali digunakan dalam analisis dan pengambilan keputusan terkait harga. Artikel ini akan membahas bagaimana matematika digunakan dalam mencari harga yang optimal, baik dari sudut pandang konsumen maupun produsen.
1. Analisis Permintaan dan Penawaran
Salah satu pendekatan matematis yang paling umum digunakan dalam menentukan harga adalah analisis permintaan dan penawaran. Dalam analisis ini, fungsi-fungsi matematis digunakan untuk menggambarkan bagaimana harga memengaruhi jumlah barang yang diminta dan ditawarkan di pasar.
Permintaan (Qd) dan penawaran (Qs) dapat diungkapkan sebagai fungsi-fungsi matematis:
Qd=a−bP
Qs=c+dP
Dalam persamaan di atas, P adalah harga, Qd adalah jumlah yang diminta, Qs adalah jumlah yang ditawarkan, dan a, b, c, dan d adalah parameter yang mencerminkan karakteristik pasar dan produk. Analisis matematis ini memungkinkan produsen untuk mencari harga yang memaksimalkan keuntungan mereka, sementara konsumen dapat menemukan harga yang mereka anggap paling cocok dengan anggaran mereka.
2. Diskon dan Potongan Harga
Ketika konsumen mencari harga yang lebih terjangkau, diskon dan potongan harga adalah elemen penting. Dalam hal ini, matematika digunakan untuk menghitung diskon dan potongan harga yang akan memberikan harga terendah. Misalnya, jika sebuah produk memiliki harga asli P, dan ada diskon sebesar X% yang diberikan, maka harga setelah diskon (Pdiskon) dapat dihitung dengan rumus:
Pdiskon=P−100XP
Pendekatan matematis ini memungkinkan konsumen untuk dengan cepat menghitung harga terbaik setelah diskon, membantu mereka membuat keputusan belanja yang cerdas.
3. Penentuan Harga Optimal untuk Keuntungan
Dari perspektif produsen, matematika digunakan untuk menentukan harga optimal yang akan menghasilkan keuntungan maksimal. Ini melibatkan perhitungan biaya produksi, margin keuntungan, dan elastisitas permintaan. Penentuan harga optimal ini sering kali melibatkan optimisasi matematis, yang dapat memerlukan solusi numerik atau analisis statistik yang canggih.
4. Strategi Penetapan Harga Dinamis
Penetapan harga dinamis adalah strategi di mana harga produk berubah berdasarkan faktor-faktor seperti permintaan saat itu, persediaan, atau preferensi pelanggan. Analisis matematis dan algoritma di balik sistem ini dapat sangat kompleks. Matematika memainkan peran penting dalam mengidentifikasi faktor-faktor yang memengaruhi perubahan harga dan menentukan cara terbaik untuk mengelola harga secara dinamis.
5. Pemodelan Analisis Sentimen dan Penetapan Harga
Dalam era digital saat ini, data sosial media dan analisis sentimen semakin banyak digunakan untuk memahami bagaimana persepsi pelanggan memengaruhi harga produk. Metode analisis matematis seperti pengolahan bahasa alami (NLP) digunakan untuk menganalisis ulasan pelanggan dan memprediksi bagaimana perubahan harga dapat memengaruhi persepsi pelanggan.
Penutup
Mencari harga dengan pendekatan matematis adalah alat yang penting dalam ekonomi dan dunia bisnis modern. Dari analisis permintaan dan penawaran hingga strategi penetapan harga yang lebih kompleks, matematika membantu produsen dan konsumen untuk membuat keputusan yang lebih baik terkait harga. Dengan data yang semakin banyak dan kemajuan dalam analisis matematis, kita dapat mengharapkan bahwa matematika akan terus menjadi alat yang kuat dalam mencari harga yang optimal.
Modul Belajar Mandiri: Bidang Studi Ilmu Pengetahuan Sosial - Ekonomi

